Guía Completa para Resolver Problemas de Estados Absorbentes en Cadenas de Markov

Arturo

18/03/2025 - Actualizado: 26/03/2025

Tabla de Contenidos:

Generador de Matriz con estado absorbente de Markov

Nota: para usar esta calculadora, la matriz de transicion debe estar debidamente organizada, en este orden:

matriz transicion

Calculadora de Cadenas de Markov

Calculadora de Cadenas de Markov con Estados Absorbentes

Introduce la matriz de transición P (dimensiones de 2×2 hasta 6×6):

Cadenas de Markov: Guía Completa y Práctica para Entenderlas Fácilmente

Las cadenas de Markov con estados absorbentes son una herramienta fundamental en la modelación de procesos estocásticos, en los que ciertos estados actúan como "trampas" en las que, una vez ingresados, el proceso no puede salir. En esta guía te presentamos 4 pasos esenciales para resolver este tipo de problemas, ilustrándolos con ejemplos prácticos.

Estados Absorbentes

Una cadena de Markov describe la evolución de un sistema en pasos discretos, en el que la probabilidad de transitar a otro estado depende únicamente del estado actual. En algunos casos, el sistema contiene estados absorbentes: estados que, al alcanzarlos, el proceso se detiene.

Para resolver problemas de este tipo se deben calcular dos matrices clave:

Cómo Resolver Cadenas de Markov en Estado Estable: Guía Paso a Paso
  • La matriz fundamental N = (I - Q)^{-1}, que indica el número esperado de visitas a los estados transitorios antes de ser absorbido.
  • La matriz de absorción B = (N * R), que muestra la probabilidad de terminar en cada estado absorbente.

A continuación, se detalla el proceso en 4 pasos, acompañado de ejemplos.

Paso 1. Identificar los estados absorbentes

Definición: Un estado i es absorbente si la probabilidad de permanecer en él una vez que se entra es 1, es decir, si

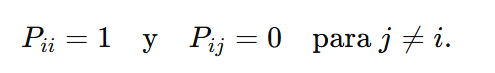
Identificar los estados absorbentes
Procedimiento:

Predicción a Corto Plazo con Cadenas de Markov: Una Guía Paso a Paso
  • Inspecciona cada fila de la matriz de transición P.
  • Si encuentras una fila cuyo valor en la diagonal es 1 y el resto de valores en esa fila es 0, ese estado es absorbente.

Por ejemplo, si tienes una matriz de transición como:

matriz de transicion

El tercer estado es absorbente (porque P33 = 1 y P3j = 0 para j ≠ 3).

El cuarto estado no es absorbente, porque P44 = 0.7, pero no es 1 (y hay otras transiciones salientes).

Paso 2. Reordenar la matriz de transición y extraer Q, R, O, I

Para poder aplicar la teoría de estados absorbentes, se suele reordenar la matriz de transición de modo que:

  • Primero aparezcan todos los estados transitorios.
  • Después aparezcan todos los estados absorbentes.

En esa forma canónica, la matriz de transición P queda dividida en cuatro bloques:

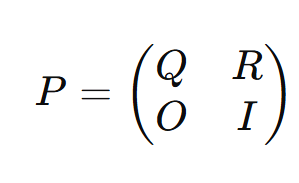
reordenar la matriz de transicion

donde:

  • Q es la submatriz (de dimensión t×t, siendo t = (número de estados transitorios)) que describe las probabilidades de ir de un estado transitorio a otro estado transitorio.
  • R es la submatriz (de dimensión t×m) que describe las probabilidades de ir de un estado transitorio a un estado absorbente (m = número de estados absorbentes).
  • O es una matriz (de dimensión m×t) que, en la mayoría de los casos, es la matriz cero, pues normalmente se asume que de un estado absorbente no se sale a uno transitorio.
  • I es la matriz identidad (de dimensión m×m) que describe las transiciones de un estado absorbente a sí mismo.

Continuando con el ejemplo anterior:

Supongamos que el tercer estado es el único absorbente. Al reordenar para poner primero los estados transitorios (1, 2, 4) y último el estado absorbente (3), la matriz P se reescribe como:

Preordenada =

P11P12P14P13
P21P22P24P23
P41P42P44P43
P31P32P34P33

=

QR
OI

donde:

  • ( Q ): Probabilidades de transición entre estados transitorios.
  • ( R ): Probabilidades de transitar de un estado transitorio a un estado absorbente.
  • ( O ): Generalmente una matriz de ceros, pues describe las transiciones de estados absorbentes a transitorios.
  • ( I ): Matriz identidad para los estados absorbentes.

Paso 3. Calcular la matriz fundamental N = (I−Q)−1

Definición:

N = (I−Q)−1 se conoce como la matriz fundamental. Cada elemento Nij de esta matriz indica el número esperado de veces que el proceso estará en el estado transitorio j si empieza en el estado transitorio i, antes de ser absorbido.

Cálculo (Gauss-Jordan u otro método de inversión de matrices):

  1. Se construye la matriz (I−Q).
  2. Se aplica el método de Gauss-Jordan (o cualquier otro método de inversión) para hallar su inversa.
  3. El resultado es N.

Comentario: Si Q es de dimensión t×t, entonces (I−Q) también es t×t, y su inversa N mantiene esa misma dimensión.

Paso 4. Calcular la matriz de probabilidad de absorción B = N·R

Una vez obtenida N, podemos determinar la probabilidad de que, partiendo de un estado transitorio i, el proceso sea absorbido en alguno de los estados absorbentes. Para ello:

B = N·R

  • Cada fila de B corresponde a un estado transitorio.
  • Cada columna de B corresponde a un estado absorbente.
  • Por lo tanto, Bij es la probabilidad de que empezando en el estado transitorio i, finalmente se termine en el estado absorbente j.

Interpretación:

  • Si hay más de un estado absorbente, B te da la distribución de probabilidades de cuál de todos esos estados absorberá finalmente el proceso.
  • Si solo hay un estado absorbente, B será simplemente un vector columna con las probabilidades de terminar en ese estado único.
Conclusión
En resumen, la metodología para resolver problemas de cadenas de Markov con estados absorbentes se basa en los siguientes 4 pasos fundamentales:
  1. Identificar los estados absorbentes: Examina cada fila de la matriz ( P ) para detectar aquellas que tienen ( P_{ii} = 1 ) y ceros en el resto.
  2. Reordenar la matriz y extraer las submatrices ( Q ), ( R ), ( O ) e ( I ): Coloca los estados transitorios al inicio y los absorbentes al final para facilitar la manipulación.
  3. Calcular la matriz fundamental ( mathbf{N} = (I - Q)^{-1} ): Resta ( Q ) de la matriz identidad y utiliza el método de Gauss-Jordan para invertir el resultado.
  4. Calcular la matriz de absorción ( mathbf{B} = mathbf{N} , R ): Multiplica la matriz fundamental ( N ) por ( R ) para obtener las probabilidades de absorción.
Los ejemplos presentados, tanto para una matriz 3×3 como para una 4×4, ilustran claramente cada uno de estos pasos y demuestran cómo, a través de esta metodología, se puede determinar que el proceso, partiendo de cualquier estado transitorio, terminará en el estado absorbente.
¡Practica con diferentes matrices y descubre cómo varían los resultados según la estructura de transición! Esta técnica es aplicable en diversas áreas, como la ingeniería, la economía y las ciencias de la computación, donde la modelación de procesos estocásticos es fundamental.
 Calculadora de Cadenas de Markov
Calculadora de Cadenas de Markov con Estados Absorbentes
Introduce la matriz de transición P (dimensiones de 2×2 hasta 6×6):
  
 
  
 
Arturo
Ingeniero Industrial con más de dos décadas de experiencia en el sector manufacturero, especializado en gestión de calidad, seguridad ocupacional, control de inventarios y optimización de procesos. Su trayectoria abarca roles clave desde Ingeniería de Métodos hasta Gerencia de Seguridad y Mantenimiento, liderando implementaciones exitosas de sistemas ISO 9001 e ISO 27001. Experto en industrias textiles y de fabricación, integrando conceptos de ingeniería industrial con prácticas de gestión operativa avanzadas. Docente universitario en áreas de ingeniería industrial. Fundador de aprendeindustrial.com, una plataforma digital que ofrece recursos, artículos y estudios de caso sobre mejores prácticas en ingeniería industrial, seguridad ocupacional y optimización de procesos para profesionales y estudiantes y áreas en general.
  
  
Te Puede Interesar:
 Go up