Verdadera magnitud de un plano: Ejemplo práctico explicado

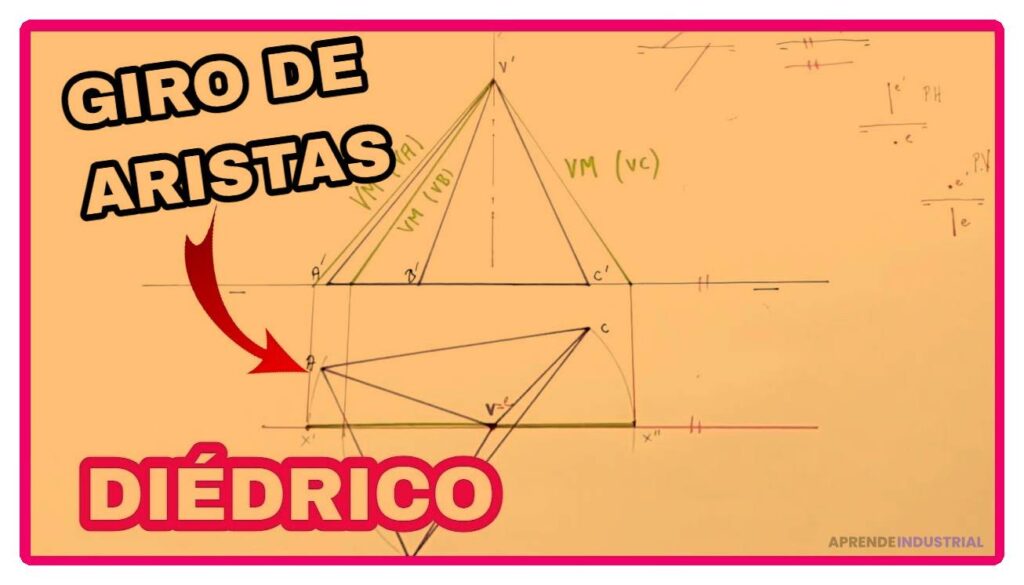
La verdadera magnitud de un plano es un concepto fundamental en el ámbito de la geometría y el dibujo técnico. Este tema es crucial para ingenieros, arquitectos y diseñadores, ya que permite representar de manera precisa las dimensiones y formas de los objetos en un espacio tridimensional. En este artículo, exploraremos en profundidad cómo determinar la verdadera magnitud de un plano, utilizando ejemplos prácticos y explicaciones detalladas que facilitarán la comprensión del proceso.

El objetivo de este artículo es proporcionar una guía completa sobre la verdadera magnitud de un plano, comenzando con la verdadera magnitud de una recta y luego extendiéndonos a la magnitud de un plano. A través de un enfoque paso a paso, se explicarán los métodos de proyección y medición, así como la importancia de las diferentes vistas en el dibujo técnico. Al final, se ofrecerán reflexiones sobre la relevancia de estos conceptos en la práctica profesional y se responderán algunas preguntas frecuentes que pueden surgir en el proceso de aprendizaje.

La verdadera magnitud de una recta

La verdadera magnitud de una recta es el primer paso para entender cómo se relacionan las dimensiones en un espacio tridimensional. Para calcularla, es esencial contar con las vistas frontal y horizontal superior de la recta. Estas vistas nos proporcionan la información necesaria para realizar las proyecciones adecuadas.

Proyección de los extremos de la recta

Para comenzar, se deben identificar los extremos de la recta en las vistas frontal y horizontal. Una vez que se tienen estas posiciones, se procede a proyectar los extremos hacia un plano paralelo. Este proceso implica trazar líneas perpendiculares desde los extremos de la recta en la vista frontal hasta el plano paralelo que se ha definido. La intersección de estas líneas con el plano paralelo nos dará los puntos que se utilizarán para calcular la verdadera magnitud.

Es importante tener en cuenta que la precisión en la proyección es fundamental. Cualquier error en la medición o en la proyección puede llevar a resultados incorrectos. Por lo tanto, se recomienda utilizar herramientas de medición adecuadas y realizar las proyecciones con cuidado. Una vez que se han proyectado los extremos, se pueden tomar las medidas necesarias para determinar la longitud de la recta en su verdadera magnitud.

Cálculo de la verdadera magnitud

Una vez que se han proyectado los extremos de la recta y se han marcado los puntos en el plano paralelo, el siguiente paso es calcular la verdadera magnitud. Para ello, se mide la distancia entre los dos puntos proyectados. En nuestro ejemplo práctico, esta distancia resultó ser de 98.6 unidades. Este valor representa la longitud real de la recta en el espacio tridimensional.

Es crucial recordar que la verdadera magnitud de una recta puede variar dependiendo de su orientación en el espacio. Por lo tanto, es fundamental realizar este proceso para cada recta que se desee analizar. La comprensión de la verdadera magnitud de una recta es esencial para el diseño y la construcción, ya que permite a los profesionales trabajar con medidas precisas y evitar errores en la ejecución de proyectos.

La verdadera magnitud de un plano

Una vez que hemos comprendido cómo calcular la verdadera magnitud de una recta, el siguiente paso es abordar la verdadera magnitud de un plano. Este proceso es similar al de la recta, pero involucra la proyección de múltiples puntos y la creación de líneas paralelas.

Proyección de puntos en el plano

Para determinar la verdadera magnitud de un plano, es necesario identificar varios puntos en el mismo. Estos puntos pueden ser los vértices de un polígono o cualquier otro punto relevante en el plano. Al igual que en el caso de la recta, se deben proyectar estos puntos hacia un plano paralelo. Esto se realiza trazando líneas perpendiculares desde cada punto en la vista frontal hasta el plano paralelo.

La proyección de los puntos es un proceso que requiere atención al detalle. Cada punto debe ser proyectado con precisión para garantizar que las medidas finales sean correctas. Una vez que se han proyectado todos los puntos, se pueden unir para formar el contorno del plano en su verdadera magnitud.

Creación de líneas paralelas

Después de proyectar los puntos y unirlos, el siguiente paso es crear líneas paralelas que representen la verdadera magnitud del plano. Estas líneas se dibujan a partir de los puntos proyectados y deben ser paralelas a las líneas originales en el plano. La creación de estas líneas es esencial para visualizar la verdadera magnitud del plano en el espacio tridimensional.

Es importante destacar que, al igual que con la recta, la orientación del plano puede afectar su verdadera magnitud. Por lo tanto, es recomendable realizar este proceso para cada plano que se desee analizar. La correcta representación de la verdadera magnitud de un plano es fundamental para la elaboración de planos técnicos y la ejecución de proyectos de construcción.

Importancia de las diferentes vistas

En el dibujo técnico, las diferentes vistas juegan un papel crucial en la representación de objetos tridimensionales. Las vistas frontal, lateral y superior son esenciales para comprender la forma y las dimensiones de un objeto. En el contexto de la verdadera magnitud, estas vistas permiten realizar proyecciones precisas y obtener medidas exactas.

Vistas frontal y horizontal

La vista frontal es la representación del objeto desde un ángulo de 90 grados, mientras que la vista horizontal muestra el objeto desde arriba. Ambas vistas son necesarias para calcular la verdadera magnitud de una recta o un plano. Al observar estas vistas, se pueden identificar las dimensiones y las proporciones del objeto, lo que facilita la proyección de puntos y la creación de líneas paralelas.

Además, es importante considerar que la elección de la vista puede influir en la percepción del objeto. Por ejemplo, un objeto puede parecer más largo o más corto dependiendo del ángulo desde el cual se observe. Por lo tanto, es fundamental utilizar las vistas adecuadas para obtener una representación precisa de la verdadera magnitud.

Vistas laterales y perspectivas

Las vistas laterales también son importantes, ya que proporcionan información adicional sobre la forma del objeto. Estas vistas permiten observar detalles que pueden no ser evidentes en las vistas frontal y horizontal. Al incluir vistas laterales en el análisis, se puede obtener una comprensión más completa de la verdadera magnitud del objeto.

Por otro lado, las perspectivas son representaciones tridimensionales que pueden ayudar a visualizar la verdadera magnitud de un objeto en un contexto más realista. Aunque las perspectivas no son utilizadas directamente para calcular la verdadera magnitud, pueden ser útiles para comunicar ideas y conceptos a otros profesionales en el campo del diseño y la construcción.

Proceso de medición y cálculo

El proceso de medición y cálculo es fundamental para determinar la verdadera magnitud de una recta o un plano. Este proceso implica la utilización de herramientas de medición y técnicas de cálculo que garantizan la precisión de los resultados.

Herramientas de medición

Existen diversas herramientas de medición que se pueden utilizar en el proceso de cálculo de la verdadera magnitud. Entre ellas se encuentran las reglas, calibradores y transportadores. Cada una de estas herramientas tiene su propia función y es importante elegir la adecuada según el tipo de medición que se desee realizar.

Por ejemplo, una regla es ideal para medir distancias lineales, mientras que un calibrador es útil para medir diámetros y profundidades. La elección de la herramienta correcta puede marcar la diferencia en la precisión de las medidas obtenidas. Además, es recomendable realizar varias mediciones y promediar los resultados para minimizar errores.

Técnicas de cálculo

Una vez que se han tomado las medidas, el siguiente paso es realizar los cálculos necesarios para determinar la verdadera magnitud. Esto puede incluir la aplicación de fórmulas matemáticas y la utilización de software de diseño asistido por computadora (CAD) que facilite el proceso.

Es importante tener en cuenta que, en algunos casos, puede ser necesario realizar cálculos adicionales para obtener resultados más precisos. Por ejemplo, si se trabaja con ángulos o superficies irregulares, puede ser necesario aplicar fórmulas trigonométricas o geométricas para calcular la verdadera magnitud de manera efectiva.

Casos especiales: rectas perpendiculares

En algunos casos, una recta puede ser perpendicular al plano, lo que puede simplificar el proceso de cálculo de su verdadera magnitud. Cuando una recta es perpendicular, su longitud en el plano es igual a su verdadera magnitud.

Identificación de rectas perpendiculares

Para identificar si una recta es perpendicular a un plano, es necesario analizar las vistas del objeto. Si la recta forma un ángulo de 90 grados con el plano en cuestión, se considera perpendicular. Esta identificación es crucial, ya que permite simplificar el proceso de cálculo y obtener resultados más rápidos.

Una vez que se ha identificado una recta perpendicular, se puede proceder a medir su longitud directamente en la vista correspondiente. Esto elimina la necesidad de realizar proyecciones y cálculos adicionales, lo que ahorra tiempo y esfuerzo en el proceso.

Ventajas de trabajar con rectas perpendiculares

Trabajar con rectas perpendiculares ofrece varias ventajas en el ámbito del diseño y la construcción. En primer lugar, la simplicidad del cálculo permite a los profesionales obtener resultados más rápidos y precisos. Además, las rectas perpendiculares son comunes en la arquitectura y la ingeniería, lo que significa que este tipo de análisis es frecuente en proyectos reales.

Por otro lado, la identificación de rectas perpendiculares también puede ayudar a evitar errores en la ejecución de proyectos. Al trabajar con medidas precisas y simplificadas, se reduce el riesgo de cometer errores que puedan afectar la calidad del trabajo final.

Ejemplo práctico de cálculo

Para ilustrar el proceso de cálculo de la verdadera magnitud de un plano, presentaremos un ejemplo práctico que abarca todos los pasos necesarios. Este ejemplo servirá como guía para aquellos que deseen aplicar estos conceptos en su trabajo.

Descripción del ejemplo

Supongamos que tenemos un plano rectangular con vértices en las siguientes coordenadas: A(0,0), B(0,50), C(100,50) y D(100,0). Nuestro objetivo es calcular la verdadera magnitud de este plano utilizando las técnicas de proyección y medición que hemos discutido anteriormente.

Proceso de cálculo

1. Identificación de puntos: Comenzamos identificando los puntos A, B, C y D en la vista frontal y horizontal del plano. Estos puntos nos servirán como base para las proyecciones.

2. Proyección de puntos: A continuación, proyectamos cada uno de los puntos hacia un plano paralelo. Esto implica trazar líneas perpendiculares desde cada punto en la vista frontal hasta el plano paralelo.

3. Medición de distancias: Una vez que hemos proyectado los puntos, medimos las distancias entre ellos. En este caso, la longitud del plano en su verdadera magnitud se puede calcular como la distancia entre los puntos A y C, que resulta ser de 100 unidades.

4. Representación gráfica: Finalmente, representamos gráficamente el plano en su verdadera magnitud, uniendo los puntos proyectados y creando líneas paralelas que reflejen la forma del plano original.

Este ejemplo práctico demuestra cómo aplicar los conceptos de verdadera magnitud en un contexto real, facilitando la comprensión del proceso y su relevancia en el diseño técnico.

Conclusión

La verdadera magnitud de un plano es un concepto esencial en el campo de la geometría y el dibujo técnico. A través de la proyección de puntos y la medición precisa, es posible obtener representaciones exactas de objetos en un espacio tridimensional. Este proceso no solo es fundamental para ingenieros y arquitectos, sino que también es una habilidad valiosa para cualquier profesional que trabaje en el diseño y la construcción.

A lo largo de este artículo, hemos explorado en detalle cómo calcular la verdadera magnitud de una recta y un plano, así como la importancia de las diferentes vistas y herramientas de medición. Al comprender estos conceptos, los profesionales pueden mejorar la calidad de su trabajo y evitar errores en la ejecución de proyectos.

La verdadera magnitud es un aspecto crucial del diseño técnico que permite a los profesionales trabajar con precisión y confianza. Al aplicar las técnicas y métodos discutidos en este artículo, se puede lograr una representación más fiel de los objetos en el espacio, lo que resulta en un trabajo de mayor calidad y eficacia.

Preguntas Frecuentes

¿Qué es la verdadera magnitud en geometría?

La verdadera magnitud se refiere a la representación precisa de la longitud o área de un objeto en un espacio tridimensional, obtenida a través de proyecciones y mediciones.

¿Por qué es importante calcular la verdadera magnitud?

Calcular la verdadera magnitud es esencial para garantizar que las dimensiones y proporciones de un objeto sean precisas, lo que es fundamental en el diseño y la construcción.

¿Qué herramientas se utilizan para medir la verdadera magnitud?

Se utilizan herramientas como reglas, calibradores y transportadores para medir distancias y ángulos con precisión.

¿Cómo se identifica una recta perpendicular a un plano?

Una recta es perpendicular a un plano si forma un ángulo de 90 grados con él, lo que se puede determinar al analizar las vistas del objeto.

Referencias

• Verdadera magnitud | Dibujo Técnico - WordPress.com
• Pasos para hallar la verdadera magnitud del plano | PPT