Entendiendo los Métodos de Promedios Móviles: Una Guía Completa
Calculadora de Promedio Móvil
Ingresa una lista de números separados por comas:
Ingresa el tamaño de la ventana (n):
Los Métodos de Promedios Móviles son herramientas fundamentales en el análisis de series de tiempo, permitiendo suavizar las fluctuaciones a corto plazo y detectar tendencias a largo plazo.
En este artículo, exploraremos en profundidad el método de promedios móviles, su modelo matemático, aplicación y evaluación, para que tanto profesionales como principiantes puedan comprenderlo y aplicarlo en contextos como pronósticos de demanda, análisis bursátil o incluso estudios epidemiológicos.
- Modelo y Cálculo
- Definición
- Selección del Periodo (n)
- Ventajas y Desventajas
- Tipos de Demanda y Aplicaciones
- Promedio Móvil Centrado
- Pronósticos
- Evaluación del Pronóstico
- Promedio Móvil en Software
- Ejercicio 1: Promedio Móvil Simple con Números Pequeños
- Ejercicio 2: Promedio Móvil Simple con Temperaturas
- Ejercicio 3: Promedio Móvil Simple con Excel
- Promedio Móvil Ponderado (WMA)
- Promedio Móvil Exponencial (EMA)
- Comparación de Métodos
- Ejercicio: Promedio Móvil Ponderado (WMA)
- Ejercicio: Promedio Móvil Exponencial (EMA)
- Conclusión
Modelo y Cálculo
El modelo matemático del promedio móvil simple es muy similar al de una media aritmética. Se utiliza la siguiente fórmula general:
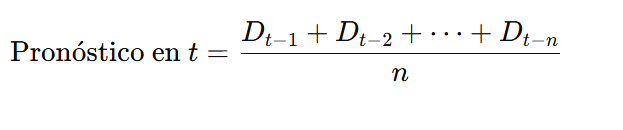
Donde:
- Dt: Datos históricos reales (por ejemplo, la demanda en el período t).
- n: Número de periodos considerados en el promedio móvil.
¿Cómo se calcula?
- Paso 1: Selecciona el número de periodos n (por ejemplo, 3 semanas o 6 semanas).
- Paso 2: Suma los datos de los n periodos inmediatos anteriores.
- Paso 3: Divide la suma entre n.
Nota: El primer pronóstico que se puede calcular depende de n. Por ejemplo, con un n=3 el primer pronóstico es para el cuarto período.
Proceso Continuo:
A medida que se disponen de nuevos datos, se descarta el dato más antiguo e incorpora el nuevo dato, moviendo la "ventana" de cálculo.
Definición
El promedio móvil simple es uno de los métodos más sencillos y efectivos para analizar series de tiempo. También se le conoce como promedio escalonado, media escalonada o promedio acumulado.
- ¿En qué consiste?
Consiste en calcular el promedio de grupos consecutivos de observaciones en una serie, lo que permite eliminar el "ruido" o fluctuaciones aleatorias de los datos. - Objetivo Principal:
Atenuar las variaciones a corto plazo para resaltar las tendencias a largo plazo. - Aplicación:
Es especialmente útil cuando la demanda o los datos analizados son relativamente estables en el tiempo (sin cambios rápidos ni patrones estacionales pronunciados). Muchos productos de consumo diario, por ejemplo, muestran estas características.
Selección del Periodo ()
La elección del número de periodos nn es crucial para el desempeño del método:
- Periodos Cortos:
Producen promedios más sensibles y responden rápidamente a cambios en la tendencia, pero pueden presentar mayor volatilidad. - Periodos Largos:
Suavizan más las fluctuaciones aleatorias, proporcionando una respuesta más uniforme, aunque con el inconveniente de retrasar la detección de tendencias emergentes.
El valor de nn no debe ser arbitrario; se debe determinar considerando la naturaleza de los datos y la rapidez con la que se desea captar la tendencia.
Ventajas y Desventajas
Ventajas
- Simplicidad Matemática:
La fórmula es sencilla y fácil de implementar. - Eliminación de Ruido:
Ayuda a eliminar fluctuaciones aleatorias, proporcionando una visión clara de la tendencia subyacente.
Desventajas
- Retraso en la Tendencia:
Si existe una tendencia fuerte, el promedio móvil tiende a retrasarla, ya que utiliza datos pasados. - Sensibilidad a la Selección de nn:
La calidad del pronóstico puede variar significativamente según el número de periodos seleccionados.
Tipos de Demanda y Aplicaciones
El promedio móvil es ideal para analizar demandas o series temporales en las que el único componente sistemático es el nivel:
- Productos de Consumo Diario:
En mercados donde la demanda es estable y no presenta crecimientos o caídas bruscas. - Mercado Bursátil:
Para rastrear tendencias en las cotizaciones de acciones. - Epidemiología:
Se puede utilizar un promedio móvil central para imputar datos faltantes o suavizar la información de brotes.
Promedio Móvil Centrado
Por defecto, los promedios móviles se asignan al período en el que se realiza el cálculo. Sin embargo, en algunos casos es deseable centrarlos:
- Promedio Móvil Central:
Se coloca el valor promedio en el centro del intervalo de tiempo, logrando una representación temporal más precisa. - Cálculo en Ventanas Impares y Pares:
- Para n impar, el primer valor se ubica en el período siguiente al inicial.
- Para n par, se calculan dos promedios (MA1 y MA2) y se promedian para colocar el valor en el centro.
Pronósticos
El método de promedio móvil se utiliza para ajustar datos y generar pronósticos:
- Pronóstico Inmediato:
El valor ajustado en el tiempo t se calcula usando la información hasta t−1. - Pronósticos a Corto Plazo:
Se utilizan los promedios móviles como valores ajustados en el origen del pronóstico. - Pronósticos Ingenuos:
Un promedio móvil de longitud uno simplemente repite el valor más reciente.
Además, para datos con tendencia, se puede aplicar el método de promedio móvil lineal (calcular promedios móviles consecutivos) para capturar el cambio de tendencia.
Evaluación del Pronóstico
Ningún pronóstico es perfecto, por lo que es importante medir su desempeño:
- Error: Diferencia entre la demanda real y el pronóstico. (Demanda real – Pronóstico)
- Error Absoluto:Valor positivo del error (ej: si el error es -2, el absoluto es 2).
- MAPE (Error Porcentual Absoluto Medio):Error porcentual promedio (ej: 5% de error es mejor que 20%).
- MAD (Desviación Media Absoluta): Mide la exactitud en las mismas unidades que la demanda.
- DCM (Desviación Cuadrática Media): Más sensible a errores grandes, ideal para detectar pronósticos inusualmente erróneos.
Ejemplo:
- Pronosticaste: 16 helados.
- Vendiste: 18 helados.
- Error absoluto: ∣18−16∣=2
La comparación de diferentes valores de n (por ejemplo, 2 periodos versus 3 periodos) puede realizarse utilizando estas medidas para seleccionar el modelo con menor error.
Promedio Móvil en Software
Hoy en día, numerosas herramientas permiten calcular promedios móviles de manera sencilla:
- Minitab, TIBCO Cloud™ Spotfire® y ArcGIS Insights:
Estas plataformas ofrecen funciones integradas para aplicar el método de promedios móviles, definiendo el tamaño del intervalo, la forma de agregación de datos y opciones para promedios móviles centrales o finales. - Aplicaciones en Excel:
Con fórmulas simples o plantillas específicas, Excel es una herramienta popular para implementar estos métodos en proyectos de pronóstico de demanda.
Ejercicio 1: Promedio Móvil Simple con Números Pequeños
Situación:
Imagina que tienes la siguiente lista de números:
5, 7, 9, 11 y 13.
Queremos calcular el promedio móvil simple usando una "ventana" de 3 números. Esto significa que vamos a sumar 3 números seguidos y luego dividir la suma entre 3. Luego, movemos la ventana una posición a la derecha y repetimos.
Paso a Paso
Primer grupo (los primeros 3 números):
- Números: 5, 7 y 9.
- Suma: 5 + 7 + 9 = 21.
- Promedio: 21 ÷ 3 = 7.
→ El primer promedio es 7.
Segundo grupo (desplazamos la ventana):
- Números: 7, 9 y 11.
- Suma: 7 + 9 + 11 = 27.
- Promedio: 27 ÷ 3 = 9.
→ El segundo promedio es 9.
Tercer grupo (desplazamos de nuevo):
- Números: 9, 11 y 13.
- Suma: 9 + 11 + 13 = 33.
- Promedio: 33 ÷ 3 = 11.
→ El tercer promedio es 11.
Resultado final: Los promedios móviles son: 7, 9 y 11.
Ejercicio 2: Promedio Móvil Simple con Temperaturas
Situación:
Imagina que cada día anotas la temperatura. Durante 7 días, las temperaturas fueron:
20°C, 22°C, 21°C, 23°C, 24°C, 22°C y 25°C.
Queremos calcular el promedio móvil simple de 3 días para ver cómo cambia la temperatura.
Paso a Paso
Primer grupo (primeros 3 días):
- Temperaturas: 20, 22 y 21.
- Suma: 20 + 22 + 21 = 63.
- Promedio: 63 ÷ 3 = 21°C.
→ El promedio de los días 1 a 3 es 21°C.
Segundo grupo (días 2, 3 y 4):
- Temperaturas: 22, 21 y 23.
- Suma: 22 + 21 + 23 = 66.
- Promedio: 66 ÷ 3 = 22°C.
→ El promedio de los días 2 a 4 es 22°C.
Tercer grupo (días 3, 4 y 5):
- Temperaturas: 21, 23 y 24.
- Suma: 21 + 23 + 24 = 68.
- Promedio: 68 ÷ 3 ≈ 22.67°C (aproximadamente 22.7°C).
→ El promedio de los días 3 a 5 es aproximadamente 22.7°C.
Cuarto grupo (días 4, 5 y 6):
- Temperaturas: 23, 24 y 22.
- Suma: 23 + 24 + 22 = 69.
- Promedio: 69 ÷ 3 = 23°C.
→ El promedio de los días 4 a 6 es 23°C.
Quinto grupo (días 5, 6 y 7):
- Temperaturas: 24, 22 y 25.
- Suma: 24 + 22 + 25 = 71.
- Promedio: 71 ÷ 3 ≈ 23.67°C (aproximadamente 23.7°C).
→ El promedio de los días 5 a 7 es aproximadamente 23.7°C.
Resultado final: Los promedios móviles son: 21°C, 22°C, 22.7°C, 23°C y 23.7°C.
Ejercicio 3: Promedio Móvil Simple con Excel
Paso 1: Configurar la Tabla de Datos
Supongamos que tienes una serie de fechas y una demanda asociada a cada fecha. En Excel, podrías organizar los datos de la siguiente manera:
| A | B | C |
|---|---|---|
| 1 | Fecha | Demanda |
| 2 | 01/01/2025 | 100 |
| 3 | 02/01/2025 | 120 |
| 4 | 03/01/2025 | 130 |
| 5 | 04/01/2025 | 140 |
| 6 | 05/01/2025 | 150 |
Nota: Asegúrate de que la columna de fecha (A) y la de demanda (B) estén correctamente formateadas.
Paso 2: Agregar la Columna del Promedio Móvil
En la columna C (o en otra columna, por ejemplo D) agregaremos el cálculo del promedio móvil simple (SMA) para 3 periodos. Debido a que el promedio de 3 periodos requiere de 3 datos, el primer pronóstico se podrá calcular en la fila 4.
Puedes simular la hoja agregando una columna nueva llamada “SMA 3”:
| A | B | C |
|---|---|---|
| 1 | Fecha | Demanda |
| 2 | 01/01/2025 | 100 |
| 3 | 02/01/2025 | 120 |
| 4 | 03/01/2025 | 130 |
| 5 | 04/01/2025 | 140 |
| 6 | 05/01/2025 | 150 |
Explicación de la fórmula:
- En la celda D4, escribimos
=PROMEDIO(B2:B4)para calcular el promedio de las demandas de las filas 2, 3 y 4. - En D5, la fórmula
=PROMEDIO(B3:B5)calcula el promedio de las filas 3, 4 y 5, y así sucesivamente.
Paso 3: Introducir las Fórmulas en Excel
Abrir Excel y crea una nueva hoja. Escribe los encabezados:
- En A1, escribe: Fecha
- En B1, escribe: Demanda
- En D1, escribe: SMA (3 periodos) (Nota: Puedes usar la columna C para otros datos y dejar la columna D para el SMA)
Ingresa los datos:
- En A2: 01/01/2025
- En B2: 100
- En A3: 02/01/2025
- En B3: 120
- En A4: 03/01/2025
- En B4: 130
- En A5: 04/01/2025
- En B5: 140
- En A6: 05/01/2025
- En B6: 150
Ingresa la fórmula para el promedio móvil:
- Selecciona la celda D4 y escribe:
=PROMEDIO(B2:B4)
Presiona Enter. Deberías ver el valor 116.67 (o 116,67 según la configuración regional).
- Selecciona la celda D5, escribe:
=PROMEDIO(B3:B5)
Presiona Enter. El resultado será 130.
- En la celda D6, escribe:
=PROMEDIO(B4:B6)
Presiona Enter. El resultado será 140.
Paso 4: Verificar y Ajustar el Formato
Redondeo:
Si deseas redondear los valores a números enteros, puedes modificar la fórmula o utilizar la función REDONDEAR. Por ejemplo, en D4 podrías escribir:
=REDONDEAR(PROMEDIO(B2:B4),0)
Esto redondeará el resultado a 0 decimales.
Formato de celda:
Selecciona las celdas con los resultados y ajusta el formato de número (clic derecho > Formato de celdas) para que muestren el número de decimales que prefieras.
Paso 5: Interpretar el Resultado
La columna SMA (3 periodos) ahora te muestra cómo se suaviza la demanda:
- D4 (116.67): Es el promedio de las demandas de 100, 120 y 130.
- D5 (130): Es el promedio de 120, 130 y 140.
- D6 (140): Es el promedio de 130, 140 y 150.
Cada celda de la columna SMA representa el promedio de los tres datos inmediatamente anteriores, permitiendo identificar tendencias y eliminar fluctuaciones aleatorias.
Resumen
- Configura tus datos: Ingresa fechas y valores de demanda en las columnas correspondientes.
- Crea la columna del promedio móvil: Usa la función
PROMEDIOpara calcular el promedio de un rango de celdas. - Arrastra la fórmula: Si tienes muchos datos, arrastra la celda con la fórmula hacia abajo para calcular el promedio móvil para cada nuevo grupo de datos.
- Ajusta el formato: Redondea o formatea los números según necesites.
Notas Adicionales
- Para otros promedios (WMA o EMA):
- WMA: Usa la función
=SUMAPRODUCTO()con pesos.
Ejemplo:=SUMAPRODUCTO(B1:B3, {0.5, 0.3, 0.2}) / SUM({0.5, 0.3, 0.2}). - EMA: Requiere cálculos recursivos. Usa la fórmula:
=α * Ventas_actual + (1-α) * EMA_anterior.
- WMA: Usa la función
- Ajusta el rango: Si tus datos empiezan en la fila 2, cambia las referencias (ej:
B2:B4). - Formato de celdas: Asegúrate de que las celdas de SMA tengan formato numérico (ej: 0 decimales).
Promedio Móvil Ponderado (WMA)
Asigna pesos mayores a los datos más recientes.
Pasos:
- Define pesos decrecientes (ejemplo: w1 > w2 > ⋯ > wn)
- Multiplica cada dato por su peso
- Suma los productos y divide entre la suma de los pesos
Fórmula:
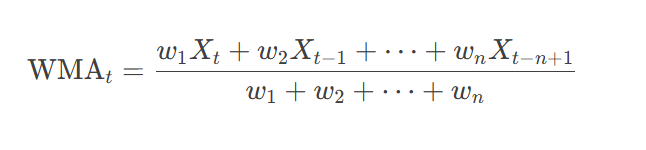
Ejemplo:
Datos: [10, 12, 14, 16, 18] (t=5) con pesos [3, 2, 1]
WMA en t=5:
(3×18 + 2×16 + 1×14) ⁄ (3+2+1) = (54 + 32 + 14) ⁄ 6 = 16.67
Promedio Móvil Exponencial (EMA)
Da más peso a los datos recientes usando un factor de suavizado (α).
Da más peso a los datos recientes usando un factor de suavizado (α).
Pasos:
- Calcula el SMA inicial para el primer período.
- Define (usualmente α= 2 / (n+1), donde n= períodos).
- Aplica recursivamente la fórmula EMA.
Fórmula:
EMAt = α⋅Xt + (1−α)⋅EMAt−1
Ejemplo:
Datos: [10, 12, 14, 16, 18] (t=5) con n=3 (α = 2/ (3+1) = 0.5)
- EMA en t=3: 0.5⋅14 + 0.5⋅12 = 13
- EMA en t=4: 0.5⋅16 + 0.5⋅13 = 14.5
- EMA en t=5: 0.5⋅18 + 0.5⋅14.5 = 16.25
Comparación de Métodos
| Método | Ventajas | Desventajas | Uso común |
|---|---|---|---|
| SMA | Simple de calcular | Retraso en señales | Tendencia general |
| WMA | Mayor peso a datos recientes | Requiere definir pesos | Análisis de corto plazo |
| EMA | Responde rápido a cambios | Complejidad de cálculo | Mercados financieros |
Ejercicio: Promedio Móvil Ponderado (WMA)
Situación: Quieres calcular cuántas galletas vendió tu mamá en 3 días, pero las ventas del último día son más importantes (peso 3), el anterior (peso 2), y el primero (peso 1).
Datos: Día 1: 5 galletas, Día 2: 7 galletas, Día 3: 9 galletas.
Pregunta: ¿Cuál es el promedio ponderado?
Paso a Paso:
- Multiplica cada día por su peso:
- Día 3: 9×3=27.
- Día 2: 7×2=14.
- Día 1: 5×1=5.
- Suma todos los resultados:
27+14+5=46. - Suma los pesos:
3+2+1=6. - Divide la suma total entre la suma de pesos:
46÷6≈7.67.
Respuesta: El promedio ponderado es ~7.67 galletas.
Ejercicio: Promedio Móvil Exponencial (EMA)
Situación: Tu hermana guardó dinero en su alcancía 4 días seguidos:
Día 1: $20, Día 2: $22, Día 3: $24, Día 4: $26.
Pregunta: Calcula el EMA para el Día 4 usando un factor de suavizado α=0.5.
Paso a Paso:
- Primero calcula el SMA para los primeros 3 días:
- Día 1, 2 y 3: (20+22+24)÷3=22.
- Fórmula EMA para el Día 4:EMADıˊa 4=0.5×26+0.5×22
- Calcula:
- 0.5×26=13.
- 0.5×22=11.
- Suma: 13+11=24.
Respuesta: El EMA para el Día 4 es $24.
¿Cómo entenderlo fácil?
- SMA: Es como hacer equipos iguales. Si sumas 3 días y divides entre 3, todos "valen lo mismo".
- WMA: Es como dar más caramelos al último día. Si el último día tiene peso 3, es el "más importante".
- EMA: Es como mezclar el nuevo dato con el promedio anterior. Si α=0.5, le das la mitad de importancia al dato nuevo y la mitad al pasado.
Conclusión
El método de promedio móvil simple es una técnica básica y poderosa para suavizar series de tiempo y generar pronósticos. Si bien su modelo matemático es sencillo y fácil de implementar, la elección adecuada del número de periodos nn y la comprensión de sus limitaciones son claves para obtener pronósticos útiles. Ya sea en el análisis de demanda de productos de consumo, seguimiento de tendencias bursátiles o en otros campos, este método ayuda a eliminar la volatilidad del "ruido" y resaltar las tendencias subyacentes.
Al combinar este método con evaluaciones de error y, en algunos casos, con métodos complementarios (como el suavizamiento exponencial o la regresión lineal), es posible obtener una herramienta robusta para la toma de decisiones basada en datos históricos.
Fuentes: es.wikipedia.org, es.wikipedia.org, gestiondeoperaciones.net





Te Puede Interesar: