Conjuntos con diagrama de venn: una guía completa y detallada

Los conjuntos con diagrama de venn son una herramienta visual fundamental en matemáticas y lógica que nos permite representar relaciones entre diferentes grupos de elementos. Estos diagramas son especialmente útiles para ilustrar conceptos de teoría de conjuntos, donde se pueden observar intersecciones, uniones y diferencias entre conjuntos. La simplicidad de su diseño los convierte en una herramienta accesible tanto para estudiantes como para profesionales que buscan entender o explicar relaciones complejas de manera clara y concisa.

En este artículo, exploraremos en profundidad qué son los diagramas de Venn, su historia, sus aplicaciones y cómo se utilizan para resolver problemas matemáticos y lógicos. A lo largo del texto, proporcionaremos ejemplos prácticos y analizaremos diferentes tipos de diagramas, así como sus características y beneficios. Espero que al final de esta lectura, tengas una comprensión sólida sobre cómo funcionan los conjuntos con diagrama de venn y cómo puedes aplicarlos en diversas situaciones.

Historia de los diagramas de Venn

Los diagramas de Venn fueron introducidos por el lógico británico John Venn en 1880, aunque sus raíces se remontan a siglos anteriores. El filósofo Ramon Llull ya había explorado conceptos similares en el año 1200, y el matemático Gottfried Wilhelm von Leibnitz también contribuyó al desarrollo de ideas relacionadas en el siglo XVII. Sin embargo, fue Leonard Euler, en el siglo XVIII, quien creó el "diagrama de Euler", considerado el precursor directo de los diagramas de Venn que conocemos hoy.

El término "diagramas de Venn" fue utilizado por primera vez por Clarence Irving Lewis en 1918, y desde entonces, estos diagramas han evolucionado gracias a las contribuciones de varios matemáticos. Por ejemplo, David W. Henderson se centró en diagramas simétricos y su relación con los números primos, mientras que A. W. F. Edwards y Branko Grunbaum trabajaron en la modificación de estos diagramas para representar un mayor número de conjuntos. Esta evolución ha permitido que los diagramas de Venn sean una herramienta versátil en matemáticas, lógica y otras disciplinas.

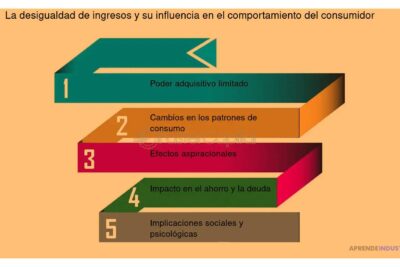
Tipos de consumos y su impacto en la economía: una guía completa

A lo largo de los años, los diagramas han sido utilizados en diversas áreas, desde la educación hasta la investigación científica. Su capacidad para simplificar conceptos complejos los convierte en una herramienta valiosa para estudiantes y profesionales por igual. En la actualidad, los conjuntos con diagrama de venn son ampliamente utilizados en la enseñanza de matemáticas y lógica, así como en la resolución de problemas en campos como la estadística y la informática.

Estructura básica de un diagrama de Venn

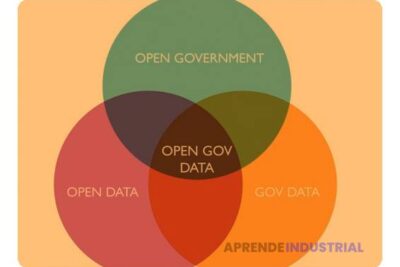
La estructura básica de un diagrama de Venn consiste en círculos que representan diferentes conjuntos. La intersección de estos círculos muestra los elementos que son comunes a los conjuntos representados. Por ejemplo, si tenemos dos conjuntos A y B, el área donde los círculos se superponen representa los elementos que pertenecen tanto a A como a B.

Los diagramas pueden variar en complejidad, desde simples diagramas de dos conjuntos hasta diagramas más complejos que representan tres o más conjuntos. En el caso de tres conjuntos, el diagrama se compone de tres círculos que se superponen, creando varias áreas que representan las diferentes combinaciones de pertenencia a los conjuntos. Esto permite visualizar relaciones más complejas y entender cómo se relacionan los diferentes grupos de elementos.

Además, los diagramas de Venn pueden incluir etiquetas y elementos específicos dentro de cada conjunto. Esto ayuda a clarificar qué elementos pertenecen a cada conjunto y cuáles son comunes entre ellos. La claridad visual que ofrecen los diagramas es una de las razones por las que son tan populares en la enseñanza y la presentación de información.

¿Qué significa filiales? Todo lo que necesitas saber

Aplicaciones de los diagramas de Venn

Los conjuntos con diagrama de venn tienen numerosas aplicaciones en diferentes campos. En matemáticas, son utilizados para enseñar conceptos de teoría de conjuntos, como la unión, la intersección y la diferencia de conjuntos. Estas operaciones son fundamentales para entender cómo se relacionan los elementos dentro de un conjunto y entre diferentes conjuntos.

En el ámbito de la lógica, los diagramas son útiles para ilustrar argumentos y relaciones lógicas. Por ejemplo, se pueden utilizar para representar premisas y conclusiones en un argumento, ayudando a visualizar la validez del mismo. Esto es especialmente valioso en la enseñanza de la lógica formal, donde la claridad en la representación de relaciones es crucial.

Además, los diagramas de Venn son ampliamente utilizados en la estadística y la investigación. Por ejemplo, pueden ayudar a visualizar la distribución de datos en diferentes categorías, lo que facilita la identificación de patrones y tendencias. También son útiles en la toma de decisiones, ya que permiten comparar diferentes opciones y evaluar sus intersecciones.

Cómo construir un diagrama de Venn

Construir un diagrama de Venn es un proceso sencillo que puede realizarse en unos pocos pasos. A continuación, te presento una guía paso a paso para crear tu propio diagrama:

Suavizacion exponencial doble: Un enfoque para pronosticar series de tiempo

1. Identifica los conjuntos: Determina qué conjuntos deseas representar. Pueden ser dos, tres o más conjuntos, dependiendo de la complejidad que desees mostrar.

2. Dibuja los círculos: Comienza dibujando un círculo para cada conjunto. Asegúrate de que los círculos se superpongan en las áreas donde haya elementos comunes.

3. Etiqueta los círculos: Asigna un nombre a cada conjunto y colócalo dentro o cerca del círculo correspondiente. Esto ayudará a identificar fácilmente qué representa cada círculo.

4. Añade los elementos: Coloca los elementos dentro de los círculos según su pertenencia a los conjuntos. Los elementos que son comunes a dos o más conjuntos deben colocarse en la intersección de los círculos.

5. Revisa y ajusta: Asegúrate de que el diagrama sea claro y fácil de entender. Ajusta la posición de los círculos y los elementos si es necesario.

Siguiendo estos pasos, podrás crear un diagrama de Venn que represente de manera efectiva las relaciones entre los conjuntos que has identificado. La práctica te ayudará a mejorar tus habilidades en la creación de estos diagramas.

Tipos de diagramas de Venn

Existen varios tipos de diagramas de Venn, cada uno diseñado para representar diferentes cantidades de conjuntos y relaciones. A continuación, describo algunos de los más comunes:

1. Diagrama de Venn de dos conjuntos: Este es el tipo más básico y consiste en dos círculos que se superponen. Es ideal para mostrar la relación entre dos grupos de elementos y permite visualizar la intersección y la diferencia entre ellos.

2. Diagrama de Venn de tres conjuntos: Este diagrama incluye tres círculos que se superponen, creando varias áreas que representan diferentes combinaciones de pertenencia. Es útil para ilustrar relaciones más complejas y se utiliza comúnmente en la enseñanza de teoría de conjuntos.

3. Diagrama de Venn extendido: Este tipo de diagrama puede incluir más de tres conjuntos y se utiliza para representar relaciones más complejas. Aunque su construcción puede ser más complicada, es una herramienta poderosa para visualizar interacciones entre múltiples grupos.

4. Diagrama de Venn en múltiples dimensiones: Algunos diagramas de Venn avanzados utilizan dimensiones adicionales para representar relaciones más complejas. Estos diagramas son menos comunes y suelen ser utilizados en investigaciones matemáticas o científicas.

Cada tipo de diagrama de Venn tiene sus propias características y aplicaciones, y la elección del tipo adecuado dependerá de la complejidad de la relación que desees representar.

Beneficios de utilizar diagramas de Venn

Los conjuntos con diagrama de venn ofrecen una serie de beneficios que los hacen especialmente útiles en la enseñanza y la presentación de información. Algunos de estos beneficios incluyen:

• Claridad visual: Los diagramas permiten representar relaciones complejas de manera clara y concisa, facilitando la comprensión de conceptos abstractos.

• Facilidad de uso: Crear un diagrama de Venn es un proceso sencillo que no requiere herramientas avanzadas. Esto lo convierte en una herramienta accesible para estudiantes y educadores.

• Versatilidad: Los diagramas pueden ser utilizados en una amplia variedad de disciplinas, desde matemáticas y lógica hasta ciencias sociales y estadísticas.

• Estimulación del pensamiento crítico: Al utilizar diagramas para analizar relaciones, los estudiantes desarrollan habilidades de pensamiento crítico y resolución de problemas.

• Facilitación del aprendizaje colaborativo: Los diagramas de Venn son herramientas efectivas para el trabajo en grupo, ya que permiten a los estudiantes colaborar en la identificación de relaciones y patrones.

Estos beneficios hacen que los diagramas de Venn sean una herramienta valiosa en el aula y en otros entornos de aprendizaje.

Ejemplos prácticos de diagramas de Venn

Para ilustrar cómo se utilizan los conjuntos con diagrama de venn, aquí hay algunos ejemplos prácticos:

1. Ejemplo de dos conjuntos: Supongamos que queremos comparar dos grupos de estudiantes: los que estudian matemáticas y los que estudian ciencias. Podemos crear un diagrama de Venn con dos círculos, uno para cada grupo. La intersección representará a los estudiantes que estudian ambas materias.

2. Ejemplo de tres conjuntos: Imaginemos que queremos analizar las preferencias de los estudiantes en cuanto a deportes, música y arte. Un diagrama de Venn de tres conjuntos nos permitirá visualizar cuántos estudiantes disfrutan de cada actividad y cuántos tienen intereses en común.

3. Ejemplo en investigación: En un estudio sobre hábitos de consumo, un investigador puede utilizar un diagrama de Venn para mostrar la relación entre diferentes grupos de consumidores, como aquellos que compran productos orgánicos, productos locales y productos sostenibles. Esto ayudará a identificar patrones y tendencias en el comportamiento de compra.

Estos ejemplos muestran cómo los diagramas de Venn pueden ser utilizados en situaciones del mundo real para facilitar la comprensión de relaciones y patrones.

Errores comunes al utilizar diagramas de Venn

A pesar de su simplicidad, hay algunos errores comunes que las personas suelen cometer al utilizar conjuntos con diagrama de venn. Aquí hay algunos de ellos:

1. No etiquetar adecuadamente: Es fundamental etiquetar cada conjunto de manera clara para evitar confusiones. La falta de etiquetas puede llevar a malentendidos sobre qué representa cada círculo.

2. Sobrecargar el diagrama: Al intentar representar demasiados conjuntos o elementos en un solo diagrama, se puede crear una imagen confusa y difícil de interpretar. Es mejor dividir la información en varios diagramas si es necesario.

3. Ignorar las intersecciones: A veces, las personas olvidan incluir las áreas de intersección, lo que puede llevar a una representación incompleta de las relaciones entre los conjuntos.

4. No revisar el diagrama: Es importante revisar el diagrama para asegurarse de que todos los elementos estén correctamente ubicados y que la representación sea clara. Un diagrama descuidado puede causar confusión.

5. No considerar el contexto: Al crear un diagrama de Venn, es esencial tener en cuenta el contexto en el que se utilizará. Un diagrama que es claro en un contexto puede no serlo en otro.

Evitar estos errores puede mejorar significativamente la efectividad de tus diagramas de Venn y facilitar la comprensión de las relaciones que deseas representar.

Ejercicios prácticos con diagramas de Venn

Para consolidar tu comprensión sobre los conjuntos con diagrama de venn, aquí hay algunos ejercicios prácticos que puedes realizar:

1. Ejercicio de dos conjuntos: Crea un diagrama de Venn para representar las preferencias de los estudiantes en cuanto a dos asignaturas, como matemáticas y literatura. Identifica cuántos estudiantes prefieren solo una asignatura, cuántos prefieren ambas y cuántos no prefieren ninguna.

2. Ejercicio de tres conjuntos: Realiza un diagrama de Venn que represente las actividades extracurriculares de los estudiantes en tu escuela. Incluye deportes, música y arte. Analiza cuántos estudiantes participan en cada actividad y cuántos participan en combinaciones de ellas.

3. Ejercicio de investigación: Investiga un tema de tu interés y utiliza un diagrama de Venn para representar las relaciones entre diferentes conceptos o categorías. Por ejemplo, si investigas sobre animales, puedes comparar mamíferos, reptiles y aves.

Estos ejercicios te ayudarán a practicar la creación y el análisis de diagramas de Venn, mejorando tu comprensión de cómo funcionan y cómo se pueden aplicar en diferentes contextos.

Conclusión

Los conjuntos con diagrama de venn son una herramienta poderosa y versátil que facilita la comprensión de relaciones complejas entre diferentes grupos de elementos. Su historia, estructura y aplicaciones en diversas disciplinas los convierten en un recurso valioso tanto en la educación como en la investigación. Al aprender a construir y utilizar estos diagramas, puedes mejorar tus habilidades de análisis y visualización, lo que te permitirá abordar problemas de manera más efectiva.

Espero que este artículo te haya proporcionado una comprensión profunda sobre los diagramas de Venn y cómo puedes aplicarlos en tu vida académica y profesional. No dudes en practicar la creación de tus propios diagramas y explorar las diversas aplicaciones que ofrecen.

Preguntas Frecuentes

¿Qué es un diagrama de Venn?

Un diagrama de Venn es una representación gráfica que muestra las relaciones entre diferentes conjuntos mediante círculos que se superponen.

¿Cuántos conjuntos se pueden representar en un diagrama de Venn?

Se pueden representar dos, tres o más conjuntos, aunque la complejidad aumenta con cada conjunto adicional.

¿Cuál es la utilidad de un diagrama de Venn?

Los diagramas de Venn son útiles para visualizar relaciones, identificar intersecciones y analizar datos en diversas disciplinas.

¿Cómo se construye un diagrama de Venn?

Para construir un diagrama de Venn, identifica los conjuntos, dibuja los círculos, etiqueta y añade los elementos correspondientes.

¿Qué errores debo evitar al crear un diagrama de Venn?

Evita no etiquetar adecuadamente, sobrecargar el diagrama, ignorar intersecciones y no revisar el diagrama antes de presentarlo.

Referencias

• ¿Qué es el Diagrama de Venn? Guía completa
• Guía Completa para Diagramas de Venn
• Diagrama de Venn: entendiendo la intersección ...