Métodos gráficos: Una guía completa sobre el método gráfico en programación lineal

La programación lineal es una herramienta fundamental en la investigación de operaciones que permite optimizar recursos limitados. Uno de los enfoques más intuitivos y visuales para resolver problemas de programación lineal es el método gráfico. Este método se utiliza principalmente para problemas que involucran dos variables, lo que permite representar gráficamente las restricciones y encontrar la solución óptima de manera visual. A pesar de sus limitaciones, como la incapacidad de manejar más de dos variables o restricciones complejas, sigue siendo una técnica valiosa en la toma de decisiones.

En este artículo, exploraremos en profundidad el método gráfico en programación lineal. Analizaremos qué es, cómo se aplica, sus ventajas y desventajas, así como ejemplos prácticos que ilustran su uso. También discutiremos herramientas modernas que han facilitado su implementación, como GeoGebra, y compararemos este método con otros enfoques. Al final, espero que tengas una comprensión clara de cómo aplicar el método gráfico en tus propios problemas de optimización.

¿Qué es el método gráfico?

El método gráfico es una técnica visual utilizada para resolver problemas de programación lineal que involucran dos variables. Esta técnica permite representar gráficamente las restricciones y la función objetivo, facilitando la identificación de la región factible y la solución óptima. A través de la representación gráfica, se pueden visualizar las interacciones entre las variables y las restricciones, lo que proporciona una comprensión más clara del problema.

La esencia del método gráfico radica en la representación de las restricciones como líneas en un plano cartesiano. Cada línea representa una restricción, y el área donde todas las restricciones se superponen se denomina región factible. La solución óptima se encuentra en uno de los vértices de esta región, lo que permite maximizar o minimizar la función objetivo.

Tecnologías RFID: ¿Qué es RFID y cómo transforman los sistemas RFID?

Es importante destacar que el método gráfico tiene limitaciones. Solo es aplicable a problemas con dos variables, lo que significa que no se puede utilizar para problemas más complejos que involucren tres o más variables. Sin embargo, su simplicidad y claridad lo convierten en una herramienta valiosa para problemas básicos de optimización.

Aplicaciones del método gráfico

El método gráfico se utiliza en una variedad de campos, incluyendo la economía, la ingeniería, la logística y la administración. Algunas de las aplicaciones más comunes incluyen:

1. Maximización de beneficios: Las empresas pueden utilizar el método gráfico para determinar la combinación óptima de productos a fabricar que maximiza sus beneficios, dadas ciertas restricciones de recursos.

2. Planificación de producción: En la industria manufacturera, este método ayuda a planificar la producción de diferentes productos, considerando limitaciones como la capacidad de la maquinaria y la disponibilidad de materiales.

   Guía completa sobre html estructura y su importancia en el diseño web

3. Distribución de recursos: Las organizaciones pueden utilizar el método gráfico para asignar recursos limitados de manera eficiente, asegurando que se satisfagan las demandas de los clientes.

4. Análisis de decisiones: En la toma de decisiones, el método gráfico permite visualizar diferentes escenarios y evaluar el impacto de diversas decisiones en los resultados.

A través de estas aplicaciones, el método gráfico demuestra ser una herramienta poderosa para la optimización y la toma de decisiones informadas.

Proceso del método gráfico

El proceso para aplicar el método gráfico se puede dividir en varios pasos clave. A continuación, describo cada uno de ellos:

La Importancia de los SGBD en la Gestión de Datos Empresariales

1. Definición de variables: El primer paso es identificar las variables que se utilizarán en el problema. Estas variables deben ser relevantes para el objetivo que se desea alcanzar.

2. Formulación de restricciones: Una vez definidas las variables, se deben establecer las restricciones que limitan las posibles soluciones. Estas restricciones pueden ser de diferentes tipos, como limitaciones de recursos o condiciones de mercado.

3. Formulación de la función objetivo: La función objetivo es la expresión matemática que se desea maximizar o minimizar. Esta función debe estar en función de las variables definidas anteriormente.

4. Graficar las restricciones: En este paso, se representan gráficamente las restricciones en un plano cartesiano. Cada restricción se convierte en una línea, y el área donde todas las líneas se superponen es la región factible.

5. Identificación de la región factible: La región factible es el área donde se cumplen todas las restricciones. Es importante identificar esta área, ya que la solución óptima se encontrará dentro de ella.

6. Evaluación de la función objetivo en los vértices: La solución óptima se encuentra evaluando la función objetivo en los vértices de la región factible. Esto implica calcular el valor de la función objetivo en cada uno de los vértices y determinar cuál de ellos proporciona el mejor resultado.

7. Selección de la solución óptima: Finalmente, se selecciona la solución óptima en función de los resultados obtenidos en el paso anterior. Esta solución representa la combinación de variables que maximiza o minimiza la función objetivo.

Este proceso proporciona un enfoque sistemático para resolver problemas de programación lineal utilizando el método gráfico.

Herramientas para aplicar el método gráfico

A lo largo de los años, han surgido diversas herramientas que facilitan la aplicación del método gráfico. Algunas de las más populares incluyen:

1. GeoGebra: Esta herramienta de matemáticas interactivas permite graficar funciones y restricciones de manera sencilla. Su interfaz intuitiva facilita la visualización de la región factible y la identificación de la solución óptima.

2. Microsoft Excel: Aunque Excel no está diseñado específicamente para la programación lineal, se pueden utilizar sus funciones gráficas para representar restricciones y evaluar la función objetivo. Además, permite realizar análisis de sensibilidad y simulaciones.

3. MATLAB: Esta plataforma de programación es ideal para resolver problemas más complejos de programación lineal. Aunque su uso puede ser más técnico, ofrece potentes herramientas para la optimización y el análisis de datos.

4. Python: Con bibliotecas como Matplotlib y SciPy, Python se ha convertido en una opción popular para resolver problemas de programación lineal. Permite crear gráficos y realizar cálculos complejos de manera eficiente.

Estas herramientas han simplificado la implementación del método gráfico y han ampliado su accesibilidad a un público más amplio.

Ejemplo práctico del método gráfico

Para ilustrar la aplicación del método gráfico, consideremos un ejemplo práctico en la fabricación de tejidos. Supongamos que una empresa produce dos tipos de tejidos: A y B. La empresa desea maximizar sus beneficios, que se definen como:

[ Z = 3A + 4B ]

Donde:
- ( A ) es la cantidad de tejido A producido.
- ( B ) es la cantidad de tejido B producido.

La empresa enfrenta las siguientes restricciones:

1. Restricción de recursos: La producción de tejido A requiere 2 horas de trabajo y la de tejido B requiere 1 hora. La empresa tiene un total de 8 horas disponibles.

   [ 2A + B leq 8 ]

2. Restricción de materiales: La producción de tejido A requiere 1 unidad de material y la de tejido B requiere 2 unidades. La empresa tiene un total de 6 unidades de material disponibles.

   [ A + 2B leq 6 ]

3. Restricción de no negatividad: No se puede producir una cantidad negativa de tejidos.

   [ A geq 0 ]
   [ B geq 0 ]

Paso 1: Graficar las restricciones

Para graficar las restricciones, primero convertimos cada una de ellas en ecuaciones:

1. ( 2A + B = 8 )
2. ( A + 2B = 6 )

A continuación, encontramos los puntos de intersección de estas líneas y graficamos las restricciones en un plano cartesiano.

Paso 2: Identificar la región factible

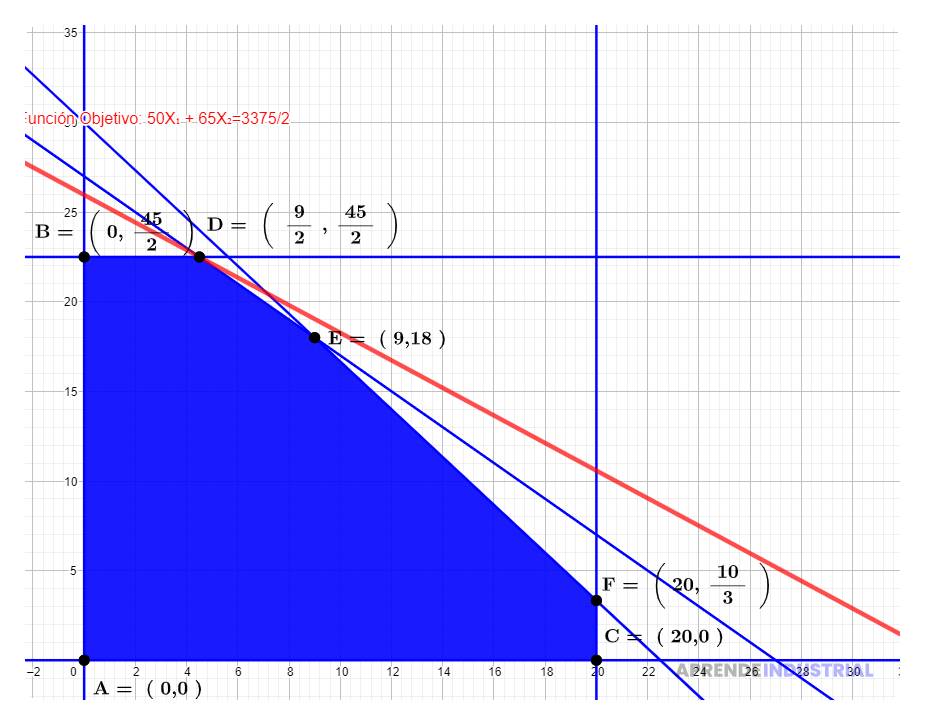
Al graficar las restricciones, encontramos que la región factible es el área donde se superponen todas las líneas. Esta área representa todas las combinaciones posibles de ( A ) y ( B ) que cumplen con las restricciones.

Paso 3: Evaluar la función objetivo

Finalmente, evaluamos la función objetivo ( Z = 3A + 4B ) en los vértices de la región factible. Supongamos que los vértices son:

• ( (0, 0) )
• ( (0, 4) )
• ( (2, 2) )
• ( (4, 0) )

Calculamos el valor de ( Z ) en cada vértice:

• En ( (0, 0) ): ( Z = 3(0) + 4(0) = 0 )
• En ( (0, 4) ): ( Z = 3(0) + 4(4) = 16 )
• En ( (2, 2) ): ( Z = 3(2) + 4(2) = 14 )
• En ( (4, 0) ): ( Z = 3(4) + 4(0) = 12 )

Paso 4: Seleccionar la solución óptima

La solución óptima se encuentra en el vértice ( (0, 4) ), donde se maximiza el beneficio a 16. Esto significa que la empresa debe producir 0 unidades de tejido A y 4 unidades de tejido B para obtener el máximo beneficio.

Ventajas y desventajas del método gráfico

El método gráfico presenta varias ventajas y desventajas que es importante considerar al aplicarlo.

Ventajas

1. Visualización clara: Permite visualizar las restricciones y la región factible, lo que facilita la comprensión del problema.

2. Simplicidad: Es un método sencillo y fácil de aplicar para problemas con dos variables.

3. Identificación rápida de soluciones: La solución óptima se puede identificar rápidamente al evaluar los vértices de la región factible.

Desventajas

1. Limitación de variables: Solo se puede aplicar a problemas con dos variables, lo que limita su uso en problemas más complejos.

2. Dificultad con restricciones complejas: Puede ser complicado graficar restricciones no lineales o múltiples restricciones.

3. No proporciona información detallada: No ofrece información sobre la sensibilidad de la solución ante cambios en las restricciones o la función objetivo.

A pesar de estas limitaciones, el método gráfico sigue siendo una herramienta valiosa en la programación lineal y la investigación de operaciones.

Comparación con otros métodos de programación lineal

Existen varios métodos para resolver problemas de programación lineal, y cada uno tiene sus propias ventajas y desventajas. A continuación, comparo el método gráfico con otros enfoques comunes:

| Método | Ventajas | Desventajas |
|---------------------------|-----------------------------------------------|-----------------------------------------------|
| Método gráfico | Visualización clara, fácil de aplicar | Limitado a dos variables, no apto para restricciones complejas |
| Método simplex | Eficiente para múltiples variables y restricciones | Más complejo de entender y aplicar |
| Método de puntos extremos | Útil para problemas de múltiples dimensiones | Puede ser tedioso y requerir cálculos extensos |
| Métodos computacionales | Capacidad para resolver problemas grandes y complejos | Requiere software especializado y conocimientos técnicos |

Cada método tiene su lugar en la programación lineal, y la elección del método adecuado depende de la naturaleza del problema y de las preferencias del analista.

Conclusión

El método gráfico es una herramienta fundamental en la programación lineal, especialmente para problemas que involucran dos variables. Su capacidad para representar gráficamente las restricciones y la función objetivo facilita la identificación de la solución óptima. A pesar de sus limitaciones, como la incapacidad de manejar problemas más complejos, sigue siendo una opción valiosa para la optimización y la toma de decisiones.

A medida que la tecnología avanza, herramientas como GeoGebra y Excel han hecho que el método gráfico sea más accesible y fácil de aplicar. Espero que este artículo te haya proporcionado una comprensión clara y detallada del método gráfico y su aplicación en la programación lineal.

Preguntas Frecuentes

¿Qué es el método gráfico en programación lineal?

El método gráfico es una técnica visual utilizada para resolver problemas de programación lineal con dos variables, permitiendo representar restricciones y encontrar la solución óptima.

¿Cuáles son las limitaciones del método gráfico?

El método gráfico solo es aplicable a problemas con dos variables y puede ser complicado para restricciones no lineales o múltiples restricciones.

¿Cómo se identifica la solución óptima en el método gráfico?

La solución óptima se identifica evaluando la función objetivo en los vértices de la región factible y seleccionando el que maximiza o minimiza el resultado.

¿Qué herramientas se pueden utilizar para aplicar el método gráfico?

Herramientas como GeoGebra, Microsoft Excel y MATLAB son populares para aplicar el método gráfico y facilitar la visualización y el análisis.

¿Es el método gráfico adecuado para todos los problemas de programación lineal?

No, el método gráfico es más adecuado para problemas simples con dos variables. Para problemas más complejos, se recomienda utilizar métodos como el simplex o herramientas computacionales.

Referencias

• Programación Lineal - Método Gráfico Investigación de ...
• Método gráfico » Programación lineal » IO
• Cap´ıtulo 2 Modelos de programación lineal. Solución ...