Todo lo que necesitas saber sobre k medias en minería de datos
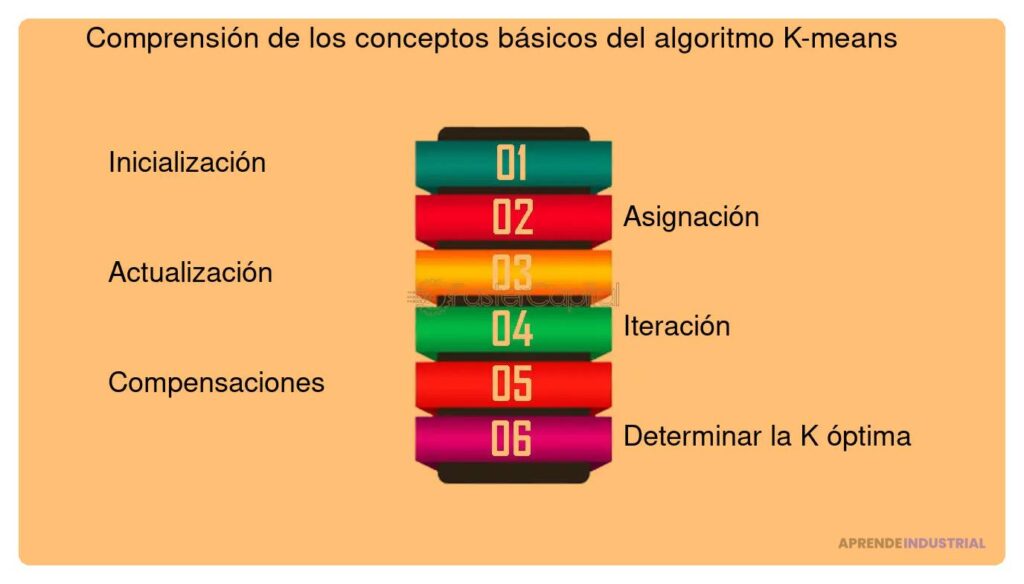
El algoritmo k medias es una de las técnicas más utilizadas en el campo de la minería de datos y el aprendizaje automático. Su principal función es agrupar un conjunto de datos en diferentes clústeres, donde los elementos dentro de cada grupo son más similares entre sí que a los de otros grupos. Esta capacidad de segmentar datos ha hecho que k medias sea una herramienta esencial en diversas aplicaciones, desde la segmentación de clientes hasta la detección de anomalías.
En este artículo, exploraremos en profundidad el funcionamiento del algoritmo k medias, sus ventajas y desventajas, así como su aplicación en diferentes áreas. También discutiremos cómo elegir el número óptimo de clústeres y ofreceremos ejemplos prácticos para ilustrar su uso. Así que, si estás interesado en aprender más sobre esta poderosa técnica, ¡sigue leyendo!
- ¿Qué es el algoritmo k medias?
- Ventajas del algoritmo k medias
- Desventajas del algoritmo k medias
- Cómo elegir el número óptimo de clústeres (k)
- Aplicaciones del algoritmo k medias
- Ejemplo práctico del algoritmo k medias
- Comparación con otros algoritmos de agrupamiento
- Consejos para mejorar el rendimiento del algoritmo k medias
- Limitaciones y consideraciones finales
- Conclusión
- Preguntas Frecuentes
- Referencias
¿Qué es el algoritmo k medias?
El algoritmo k medias es un método de agrupamiento que se utiliza para dividir un conjunto de datos en k grupos o clústeres. Cada clúster se representa mediante un centroide, que es el punto medio de todos los puntos en ese grupo. El objetivo principal es minimizar la distancia entre los puntos dentro de un clúster y su centroide, mientras se maximiza la distancia entre diferentes clústeres.
El proceso de k medias se lleva a cabo en varias iteraciones. Primero, se seleccionan k centroides iniciales de manera aleatoria. Luego, cada punto de datos se asigna al clúster cuyo centroide está más cercano. Después de que todos los puntos han sido asignados, se recalculan los centroides como el promedio de todos los puntos en cada clúster. Este proceso se repite hasta que no hay cambios significativos en la asignación de los puntos.
 El papel del arquitecto de datos en la era del Big Data
El papel del arquitecto de datos en la era del Big DataVentajas del algoritmo k medias
El algoritmo k medias tiene varias ventajas que lo hacen atractivo para los analistas de datos:
-
Simplicidad: Su implementación es relativamente sencilla, lo que permite a los usuarios entender y aplicar el algoritmo sin necesidad de conocimientos avanzados en matemáticas o estadística.
-
Rapidez: A diferencia de otros algoritmos de agrupamiento más complejos, k medias es rápido y eficiente, especialmente en conjuntos de datos grandes. Esto se debe a que el tiempo de ejecución es lineal en relación con el número de puntos de datos y clústeres.
-
Flexibilidad: Se puede aplicar a una amplia variedad de problemas, desde la segmentación de clientes hasta la clasificación de imágenes. Su versatilidad lo convierte en una herramienta valiosa en el análisis de datos.
 Diagrama de clase simbologia: Todo lo que necesitas saber
Diagrama de clase simbologia: Todo lo que necesitas saber
Sin embargo, a pesar de estas ventajas, el algoritmo k medias también presenta algunas desventajas que es importante considerar.
Desventajas del algoritmo k medias
A pesar de su popularidad, el algoritmo k medias tiene algunas limitaciones que pueden afectar su rendimiento:
-
Sensibilidad a los centroides iniciales: La elección de los centroides iniciales puede influir en el resultado final. Si se eligen de manera inadecuada, el algoritmo puede converger a un resultado subóptimo.
-
Dificultades con clústeres no esféricos: k medias asume que los clústeres tienen forma esférica y que están distribuidos uniformemente. Esto puede ser problemático en situaciones donde los clústeres tienen formas irregulares.
 LPA que es: Todo lo que necesitas saber sobre auditorías por capas
LPA que es: Todo lo que necesitas saber sobre auditorías por capas -
Número de clústeres predefinido: El usuario debe especificar el número de clústeres (k) de antemano, lo que puede ser complicado si no se tiene un conocimiento previo del conjunto de datos.
Cómo elegir el número óptimo de clústeres (k)
Elegir el número correcto de clústeres es crucial para el éxito del algoritmo k medias. Existen varios métodos que se pueden utilizar para determinar el valor óptimo de k:
-
Método del codo: Este método implica ejecutar el algoritmo para diferentes valores de k y calcular la suma de las distancias cuadradas dentro de los clústeres. Luego, se grafica esta suma en función de k y se busca el "codo" en la gráfica, que indica el punto donde la reducción de la suma se vuelve menos significativa.
-
Validación cruzada: Este enfoque implica dividir el conjunto de datos en varios subconjuntos y evaluar el rendimiento del modelo para diferentes valores de k. Se selecciona el valor que proporciona el mejor rendimiento en términos de precisión y generalización.
-
Silhouette Score: Este método evalúa la calidad de la agrupación al medir qué tan cerca están los puntos de datos de su propio clúster en comparación con otros clústeres. Un valor más alto indica una mejor separación entre clústeres.
Aplicaciones del algoritmo k medias
El algoritmo k medias se utiliza en una amplia variedad de aplicaciones en diferentes campos. Algunas de las más comunes incluyen:
-
Segmentación de clientes: Las empresas utilizan k medias para agrupar a sus clientes en función de sus comportamientos de compra, lo que les permite personalizar sus estrategias de marketing y mejorar la experiencia del cliente.
-
Clasificación de texto: En el procesamiento del lenguaje natural, k medias se utiliza para agrupar documentos o textos similares, facilitando la organización y búsqueda de información.
-
Detección de anomalías: El algoritmo puede ayudar a identificar puntos de datos que se desvían significativamente del comportamiento normal, lo que es útil en la detección de fraudes o fallos en sistemas.
Ejemplo práctico del algoritmo k medias
Para ilustrar cómo funciona el algoritmo k medias, consideremos un ejemplo práctico en el que queremos agrupar datos de ventas de una tienda. Supongamos que tenemos un conjunto de datos que incluye información sobre las compras de los clientes, como el monto gastado y la frecuencia de compra.
-
Paso 1: Elegir el número de clústeres (k). En este caso, decidimos que queremos agrupar a los clientes en 3 clústeres.
-
Paso 2: Seleccionar centroides iniciales. Elegimos aleatoriamente 3 puntos de datos como nuestros centroides iniciales.
-
Paso 3: Asignar puntos a clústeres. Cada cliente se asigna al clúster cuyo centroide está más cercano.
-
Paso 4: Recalcular centroides. Una vez que todos los clientes han sido asignados, recalculamos los centroides como el promedio de los puntos en cada clúster.
-
Paso 5: Repetir. Repetimos los pasos 3 y 4 hasta que no haya cambios significativos en la asignación de los puntos.
Al final del proceso, habremos agrupado a nuestros clientes en 3 clústeres, lo que nos permitirá analizar sus comportamientos de compra y diseñar estrategias de marketing más efectivas.
Comparación con otros algoritmos de agrupamiento
Es importante entender cómo se compara el algoritmo k medias con otros métodos de agrupamiento. A continuación, presento una tabla que resume algunas de las características clave de diferentes algoritmos de agrupamiento:
| Algoritmo | Tipo de agrupamiento | Requiere número de clústeres | Escalabilidad | Forma de clústeres |
|---|---|---|---|---|
| k medias | Particional | Sí | Alta | Esférica |
| DBSCAN | Basado en densidad | No | Media | Irregular |
| Hierárquico | Jerárquico | No | Baja | Variable |
Como se puede observar, cada algoritmo tiene sus propias ventajas y desventajas, y la elección del método adecuado dependerá del problema específico que se esté abordando.
Consejos para mejorar el rendimiento del algoritmo k medias
Si decides utilizar el algoritmo k medias, aquí hay algunos consejos que pueden ayudarte a mejorar su rendimiento:
-
Normaliza tus datos: Asegúrate de que tus datos estén normalizados para que todas las características tengan el mismo peso en el cálculo de distancias.
-
Prueba diferentes inicializaciones: Realiza múltiples ejecuciones del algoritmo con diferentes centroides iniciales para encontrar la mejor solución.
-
Utiliza técnicas de preprocesamiento: Considera aplicar técnicas como la reducción de dimensionalidad (por ejemplo, PCA) para simplificar el conjunto de datos antes de aplicar k medias.
-
Evalúa el rendimiento: Utiliza métricas como el Silhouette Score para evaluar la calidad de la agrupación y ajustar el número de clústeres según sea necesario.
-
Combina con otros métodos: En algunos casos, puede ser útil combinar k medias con otros algoritmos de agrupamiento o técnicas de aprendizaje automático para mejorar los resultados.
Limitaciones y consideraciones finales
A pesar de su utilidad, el algoritmo k medias no es una solución universal. Es importante tener en cuenta sus limitaciones y considerar otros métodos de agrupamiento cuando sea necesario. Por ejemplo, si tus datos contienen clústeres de formas irregulares o si no puedes determinar el número óptimo de clústeres, puede ser más apropiado utilizar un algoritmo como DBSCAN o un método jerárquico.
Además, siempre es recomendable realizar un análisis exploratorio de los datos antes de aplicar cualquier algoritmo de agrupamiento. Esto te permitirá comprender mejor la estructura de tus datos y tomar decisiones informadas sobre el método a utilizar.
Conclusión
El algoritmo k medias es una herramienta poderosa en el campo de la minería de datos y el aprendizaje automático. Su simplicidad y rapidez lo convierten en una opción popular para agrupar datos en diferentes clústeres. Sin embargo, es fundamental ser consciente de sus limitaciones y considerar cuidadosamente el número de clústeres a utilizar. Con un enfoque adecuado y un análisis cuidadoso, k medias puede proporcionar valiosos insights en una amplia variedad de aplicaciones.
Preguntas Frecuentes
¿Qué es el algoritmo k medias?
El algoritmo k medias es un método de agrupamiento que divide un conjunto de datos en k grupos, donde los puntos dentro de un mismo grupo son más similares entre sí.
¿Cómo se elige el número de clústeres?
Se pueden utilizar métodos como el método del codo, validación cruzada o Silhouette Score para determinar el número óptimo de clústeres.
¿Cuáles son las principales ventajas de k medias?
Las principales ventajas son su simplicidad, rapidez y flexibilidad en diversas aplicaciones.
¿Qué limitaciones tiene el algoritmo k medias?
Es sensible a los centroides iniciales, tiene dificultades con clústeres no esféricos y requiere que se especifique el número de clústeres de antemano.
¿En qué áreas se aplica k medias?
Se utiliza en segmentación de clientes, clasificación de texto, detección de anomalías y muchas otras áreas en minería de datos y machine learning.
Referencias
Deja una respuesta


Te Puede Interesar: